Hypothesis Testing III: Multiple Hypotheses and the Wald Test

Week 13

Author

Maghfira Ramadhani

Published

Nov 03, 2025

Plan

In today’s lecture, we will learn about:

  1. Testing multiple hypotheses simultaneously
  2. The Wald test for joint restrictions
  3. The interpretation of alternatives under multiple testing
  4. Example using group means from the cps dataset
  5. Mathematical practice: writing restriction matrices from hypotheses

Textbook Reference: JA 16.4

Motivation

So far, we tested a single hypothesis such as:
\[H_0: \mu_M = \mu_D\]

But sometimes we are interested in whether several population parameters are equal, for instance:
\[H_0: \mu_M = \mu_D = \mu_W = \mu_N\]


If we test each equality one-by-one using separate t-tests, we increase the chance of a Type I error (false rejection).


We therefore want a joint test that keeps the overall significance level at \(\alpha\).

Multiple Restrictions

The general setup involves \(Q\) restrictions on population parameters \(\theta_1, \theta_2, \dots, \theta_Q\).
The null hypothesis can be written as:

\[H_0: R\theta = c\]

where:

- \(R\) is a \(Q \times K\) matrix specifying which parameters are tested, and
- \(c\) is a vector of hypothesized values (often 0).

Under \(H_0\), all restrictions hold simultaneously.

The Alternative Hypothesis

The alternative to \(H_0: R\theta = c\) is:

\[H_1: R\theta \neq c\]

which means at least one restriction in \(H_0\) fails.

This is a composite alternative: it does not specify which equality fails, only that at least one does.

The Alternative Hypothesis

Example:
For the CPS example testing equal means across marital status groups:

\[ H_0: \mu_M = \mu_D = \mu_W = \mu_N \]

This can be expressed equivalently as:

\[ H_0: \begin{cases} \mu_M - \mu_D = 0 \\ \mu_D - \mu_W = 0 \\ \mu_W - \mu_N = 0 \end{cases} \]

and thus there are \(Q=3\) restrictions.
The alternative hypothesis is:

\[H_1: \text{At least one of these equalities does not hold.}\]

The Wald Test Statistic

The Wald statistic provides a general method for testing multiple restrictions.
It compares how far the estimated parameters deviate from the restrictions, relative to sampling uncertainty:

\[ W = (R\hat{\theta} - c)' [R\widehat{Var}(\hat{\theta})R']^{-1} (R\hat{\theta} - c) \]

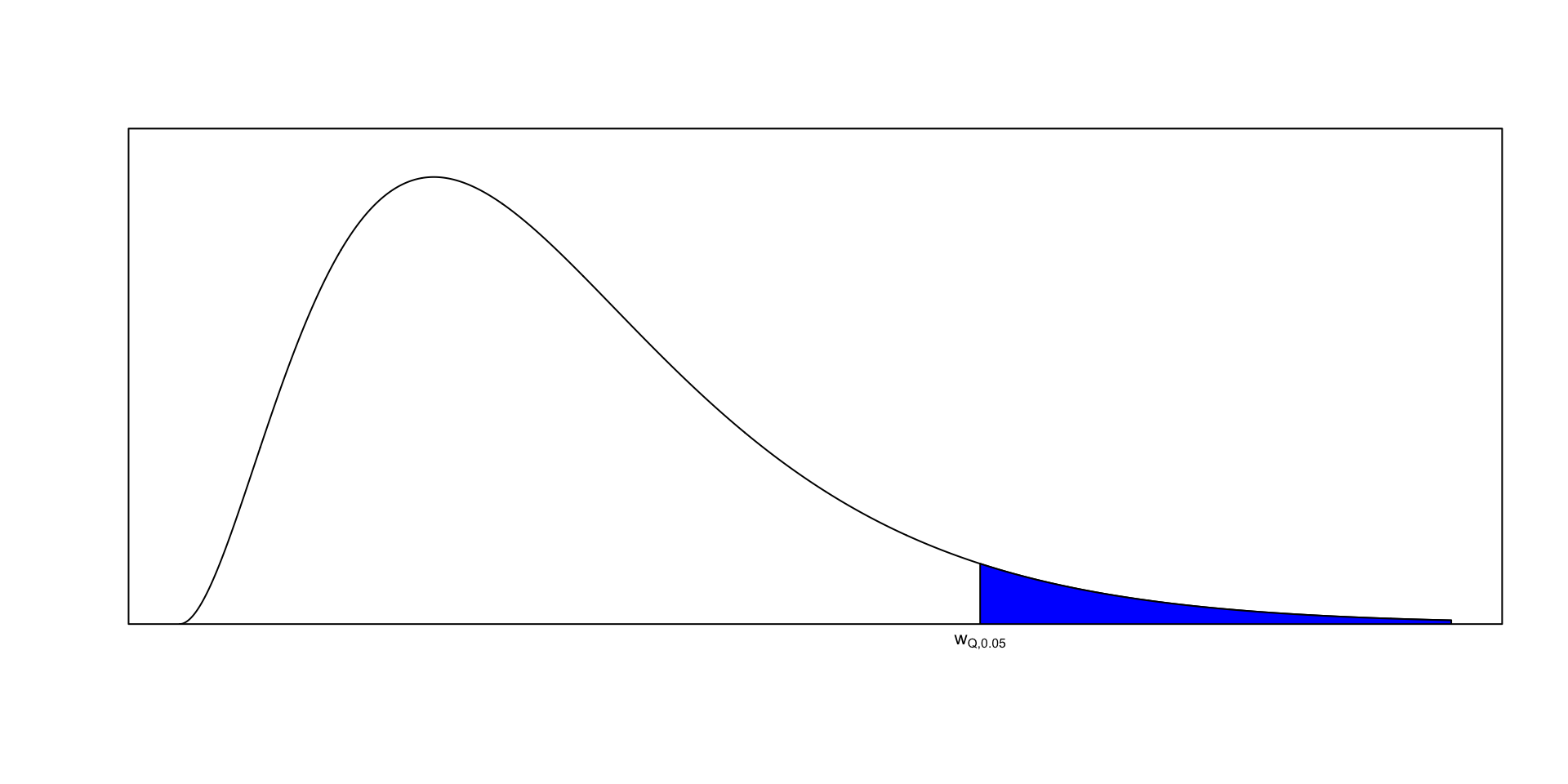
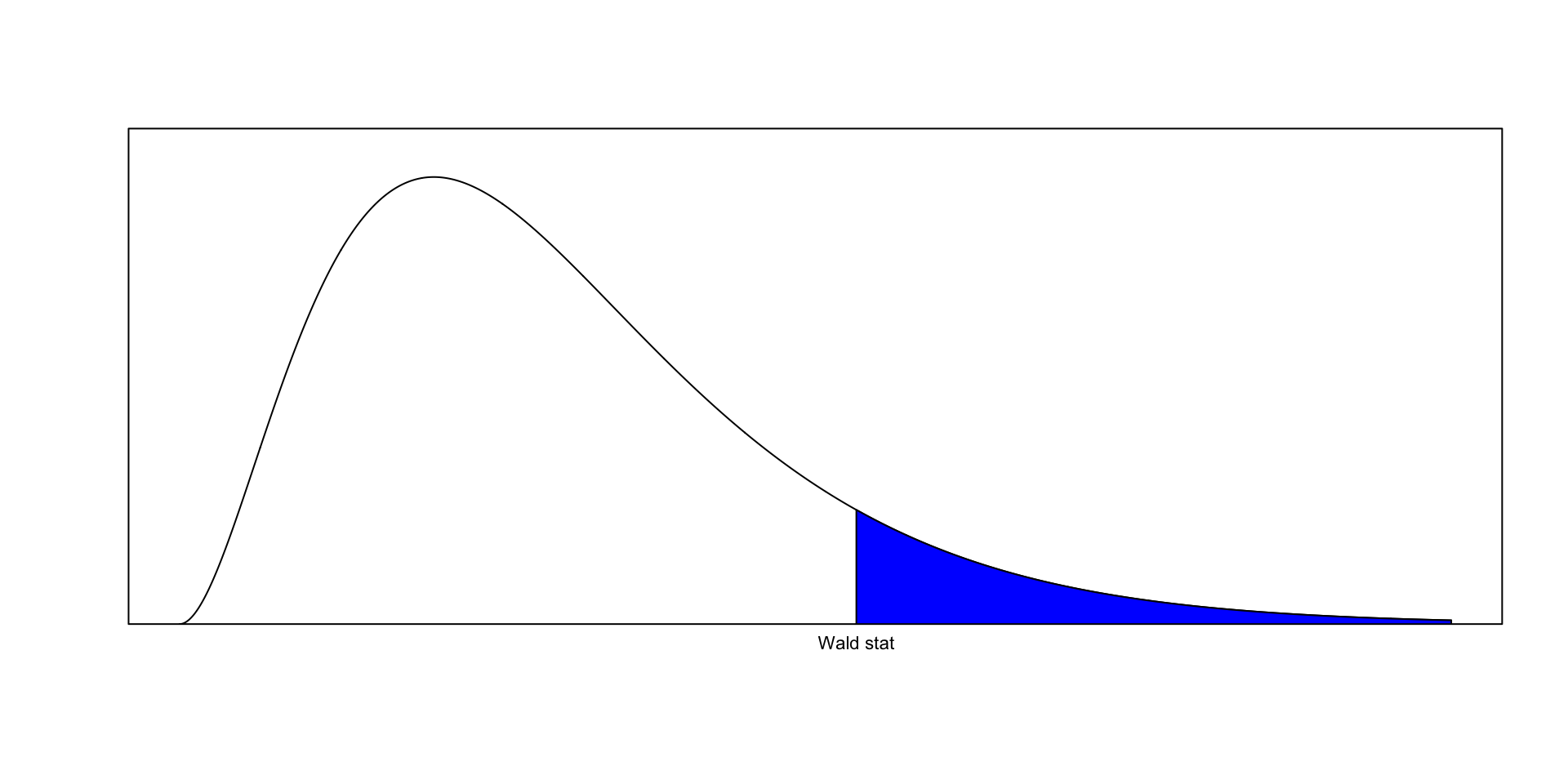
  • Under \(H_0\), \(W \sim \chi^2_Q\) approximately.
  • If \(W\) exceeds the \(1-\alpha\) quantile of \(\chi^2_Q\), we reject \(H_0\).
Rejection rule based on Wald statistic (test at \(\alpha\)-level)
  • Reject \(H_0\) if \(W > \chi^2_{Q,1-\alpha}\) or if p-value\(<\alpha\)
  • Do not reject \(H_0\) if \(W \leq \chi^2_{Q,1-\alpha}\) or if p-value\(>\alpha\)

Rejection area for Wald test

P-value of a Wald test

CPS Example: Comparing Group Means

Check Your Understanding

Question: Suppose we only compare the first three groups: Married, Divorced, and Widowed.

  1. Write the null hypothesis in the form \(H_0: R\theta = c\).
  2. Identify how many restrictions (\(Q\)) there are.
  3. Sketch or describe the shape of the rejection region in \((\mu_M, \mu_D, \mu_W)\) space.
Tip

Hint: You should find two independent restrictions when testing equality across three means.

Check Your Understanding

We use the CPS dataset from probstats4econ.
Suppose we want to test whether average weekly earnings (\(earnwk\)) are the same across four marital status groups.

\[H_0: \mu_M = \mu_D = \mu_W = \mu_N\]

data(cps)
cps_summary <- cps %>%
  group_by(marstatus) %>%
  summarise(mean_earn = mean(earnwk, na.rm=TRUE),
            sd_earn = sd(earnwk, na.rm=TRUE),
            n = n()) %>%
  mutate(se = sd_earn/sqrt(n))
cps_summary
# A tibble: 4 × 5
  marstatus     mean_earn sd_earn     n    se
  <fct>             <dbl>   <dbl> <int> <dbl>
1 Divorced           902.    714.   707  26.9
2 Married           1047.    782.  2377  16.0
3 Never married      821.    664.   853  22.8
4 Widowed            661.    327.    76  37.5

Computing the Wald Statistic

We compute the vector of sample mean differences: \[ \hat{\theta} = (\bar{Y}_M - \bar{Y}_D, \; \bar{Y}_D - \bar{Y}_W, \; \bar{Y}_W - \bar{Y}_N)' \]

and estimate its covariance matrix using the standard errors from each group mean.

Computing the Wald Statistic

# Helper functions for Wald and variance estimation
wald_test <- function(gamma_hat, var_gamma_hat, R = diag(length(gamma_hat)), r = rep(0, length(gamma_hat))) {
    if (!is.matrix(R)) R <- t(as.matrix(R))
    W <- t(R %*% gamma_hat - r) %*% solve(R %*% var_gamma_hat %*% t(R)) %*% (R %*% gamma_hat - r)
    W <- as.numeric(W)
    p_value <- 1 - pchisq(W, nrow(R))
    return(list(W = W, p_value = p_value))
}

var_mean_indep <- function(x_vectors) {
    num_means <- length(x_vectors)
    tempvec <- rep(0, num_means)
    for (i in 1:num_means) {
        tempvec[i] <- var(x_vectors[[i]]) / length(x_vectors[[i]])
    }
    var_mean <- diag(tempvec)
    return(var_mean)
}

Computing the Wald Statistic

# Prepare group data
cpsemployed<-cps%>%filter(lfstatus=="Employed")
# construct the four subsamples based on marital status
sample_m <- cpsemployed[cpsemployed$marstatus=="Married",]$earnwk
sample_d <- cpsemployed[cpsemployed$marstatus=="Divorced",]$earnwk
sample_w <- cpsemployed[cpsemployed$marstatus=="Widowed",]$earnwk
sample_n <- cpsemployed[cpsemployed$marstatus=="Never married",]$earnwk
# create a vector of the sample mean estimates
gamma_hat <- c(mean(sample_m),mean(sample_d),mean(sample_w),mean(sample_n))
# calculate the estimated asymptotic variance matrix
var_hat <- var_mean_indep(list(sample_m,sample_d,sample_w,sample_n))
gamma_hat
[1] 1046.7100  901.7475  661.0132  820.5122
var_hat
         [,1]     [,2]    [,3]     [,4]
[1,] 354.0041    0.000    0.00   0.0000
[2,]   0.0000 1076.772    0.00   0.0000
[3,]   0.0000    0.000 2675.75   0.0000
[4,]   0.0000    0.000    0.00 780.0287

Computing the Wald Statistic

# set up the linear restrictions with R and c
R <- matrix(c(1, -1, 0, 0,
              0, 1, -1, 0,
              0, 0, 1, -1),
            nrow = 3, byrow = TRUE)
c <- c(0,0,0)

# Perform Wald test
wald_test <- wald_test(gamma_hat, var_hat, R = R, c)

cat(sprintf("Wald statistic = %.3f, p-value = %.4g\n, Critical-value (5-percent) : %.3f", wald_test$W, wald_test$p_value, qchisq(0.95,2)))
Wald statistic = 80.904, p-value = 0
, Critical-value (5-percent) : 5.991

Mathematical Exercise 1

Task:
Consider the hypothesis: \[H_0: \mu_A = \mu_B = \mu_C\]

  1. Express this as a system of equalities involving mean differences.
  2. Write down the corresponding restriction matrix \(R\) if we order the means as \((\mu_A, \mu_B, \mu_C)\).
  3. What is the dimension of \(R\)? How many restrictions are being tested?
Tip

Hint: You can express it as two differences: \((\mu_A - \mu_B)\) and \((\mu_B - \mu_C)\).

Mathematical Exercise 2

Task:
Suppose we have four parameters \(\theta_1, \theta_2, \theta_3, \theta_4\) and the null hypothesis: \[H_0: \theta_1 + \theta_2 = 0, \quad \theta_3 - \theta_4 = 0\]

  1. Write this in the form \(R\theta = c\).
  2. Identify the matrix \(R\) and the constant vector \(c\).
  3. What is the number of restrictions (\(Q\))?
Tip

Hint: Think of each restriction as one row of \(R\); there are two equalities, so \(R\) will have two rows.

Exercise Solution

Exercise 1 Solution: \[ H_0: \begin{cases} \mu_A - \mu_B = 0 \\ \mu_B - \mu_C = 0 \end{cases} \] Thus, \[ R = \begin{bmatrix}1 & -1 & 0 \\ 0 & 1 & -1\end{bmatrix}, \quad c = \begin{bmatrix}0 \\ 0\end{bmatrix} \] \(R\) has 2 rows and 3 columns, so there are \(Q=2\) restrictions.

Exercise 2 Solution: \[ R = \begin{bmatrix}1 & 1 & 0 & 0 \\ 0 & 0 & 1 & -1\end{bmatrix}, \quad c = \begin{bmatrix}0 \\ 0\end{bmatrix} \] There are \(Q=2\) restrictions.

Summary & Reflection

  • The Wald test extends single-parameter testing to joint restrictions.
  • It controls the overall significance level when testing multiple equalities.
  • \(H_0: R\theta = c\) implies all restrictions hold; \(H_1\) means at least one fails.
  • Under \(H_0\), \(W \sim \chi^2_Q\) approximately.
Case Null Hypothesis Test Statistic Distribution
One restriction \(H_0: \theta = c\) t or z Normal / t
Multiple restrictions \(H_0: R\theta = c\) \(W\) \(\chi^2_Q\)
Tip

Exit Question:
Why is it misleading to test each equality separately when we are interested in all of them together?

Why is it misleading to test each equality separately when we are interested in all of them together?

  • Testing each equality at level \(\alpha\) inflates the overall Type I error rate:
    \[P(\text{at least one false rejection}) \approx 1 - (1 - \alpha)^Q\]
    For example, with \(Q = 3\) and \(\alpha = 0.05\), the overall error rate ≈ 14.2%.

  • Separate tests ignore correlations among estimates, while the Wald test accounts for their joint covariance.

  • The joint test evaluates whether all restrictions hold simultaneously, providing a single coherent decision.

  • Intuition: testing each equality separately checks individual trees; the Wald test examines the entire forest.