Expectation and Moments
Week 9
Plan
In today’s lecture, we will learn about:
- Expectation of a random variable
- Properties of expectation
- Variance and standard deviation
- Moments and their relation to mean and median
- Covariance and correlation
- Conditional expectation
Textbook Reference: SDG 4.1–4.7
Concepts
| Concept | Definition | Interpretation |
|---|---|---|
| \(E[X]\) | Mean | Long-run average |
| \(Var(X)\) | Variance | Spread around mean |
| \(Cov(X,Y)\) | Covariance | Joint variability |
| \(\rho_{XY}\) | Correlation | Strength of linear relationship |
| \(E[Y|X]\) | Conditional expectation | Best prediction of \(Y\) given \(X\) |
Expectation of a Random Variable
Expectation (or the population mean) of a random variable summarizes its central tendency.
For a discrete r.v. \(X\) with pmf \(p_X(x)\): \[E[X] = \sum_x x p_X(x)\]
For a continuous r.v. \(X\) with pdf \(f_X(x)\): \[E[X] = \int_{-\infty}^{\infty} x f_X(x) dx\]
Intuition: The expectation is the long-run average value if we repeatedly observe \(X\).
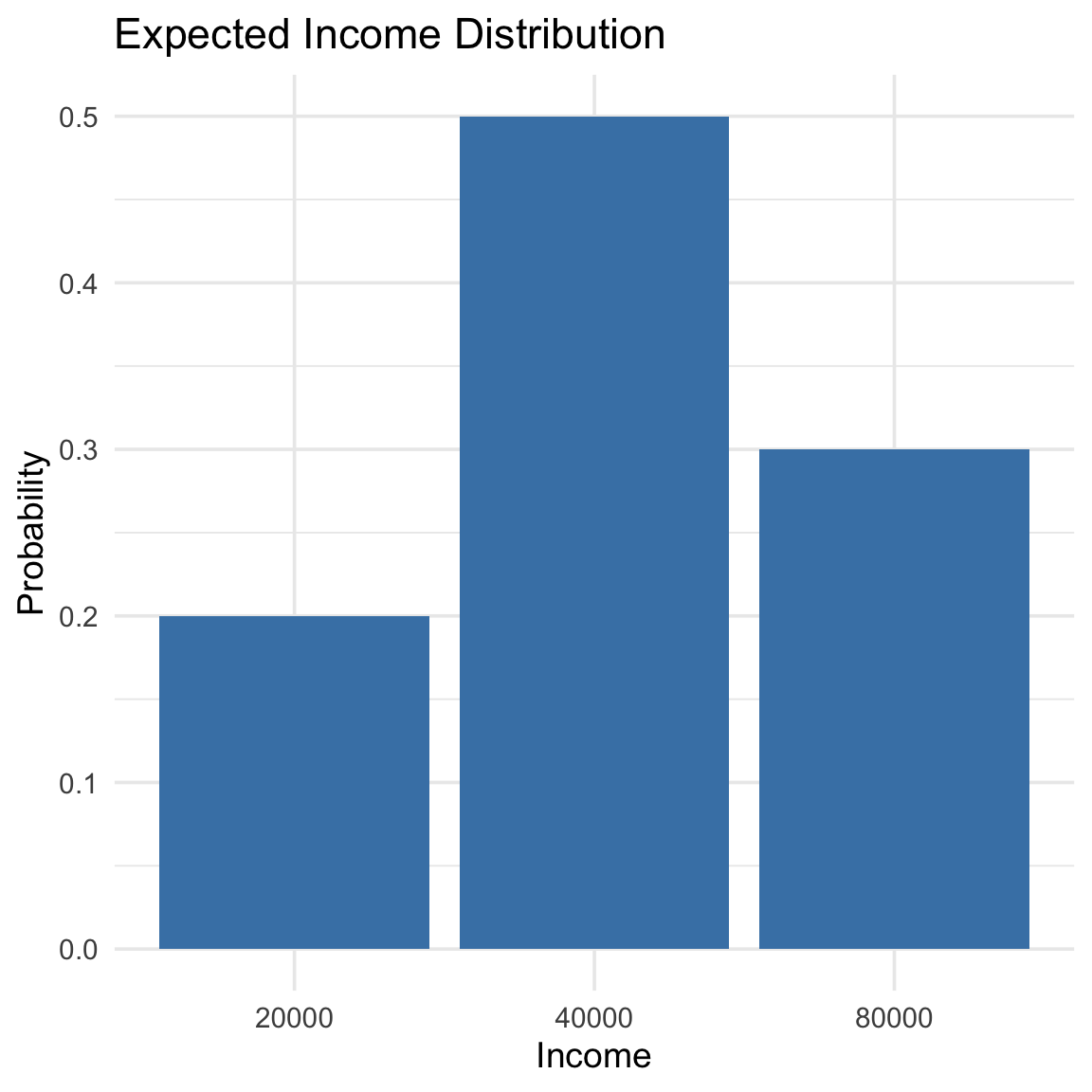
Example: Expected income
| Income (\(x\)) | Probability \(p(x)\) |
|---|---|
| 20,000 | 0.2 |
| 40,000 | 0.5 |
| 80,000 | 0.3 |
\[E[X] = 20{,}000(0.2) \\+ 40{,}000(0.5) \\+ 80{,}000(0.3) \\= 48{,}000.\]
Properties of Expectation
Let \(a,b\) be constants and \(X,Y\) random variables.
- Linearity:
\[E[aX + b] = aE[X] + b\] - Additivity:
\[E[X+Y] = E[X] + E[Y]\] - Independence:
If \(X\) and \(Y\) are independent, \(E[XY] = E[X]E[Y]\).
Application Example
A survey records the number of streaming subscriptions in 3 independent households. Let \(S_i\) be the subscriptions in household \(i\), where \(i \in \{1, 2, 3\}\). Each household has the following probability mass function (pmf): \[ P(S_i=0)=0.5,\quad P(S_i=1)=0.3,\quad P(S_i=2)=0.2. \] Let \(X = S_1 + S_2 + S_3\) be the total subscriptions across 3 independent households.
Since \(S_1,S_2,S_3\) are independent and identically distributed (i.i.d) following the given pmf, we have \[E(X)=E(S_1+S_2+S_3)=E(S_1)+E(S_2)+E(S_3)=3E(S_i).\]
Using the given pmf we can compute \(E(S_i)=\sum_{j}s_j P(S_i=s_j).\)
Variance
Variance measures the dispersion of a random variable around its mean.
\[Var(X) = E[(X - E[X])^2] = E[X^2] - (E[X])^2.\]
The standard deviation is: \[\sigma_X = \sqrt{Var(X)}.\]
Variance as Expected Squared Deviation
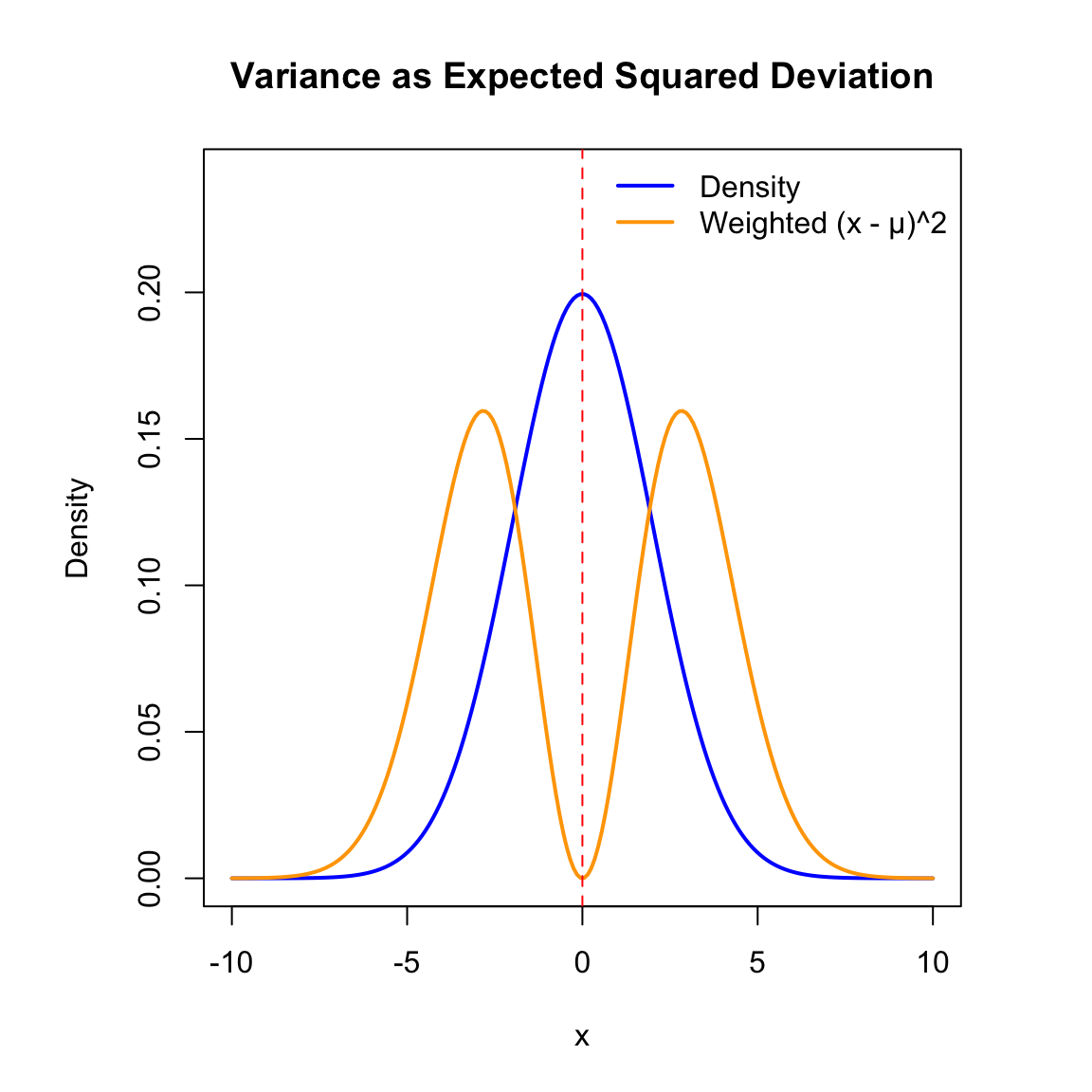
- Variance captures the expected squared distance from the mean.
- The orange curve shows how \((x - \mu)^2\) is weighted by the probability density.
- Most of the contribution to \(Var(X)\) comes from values close to the mean.
Property of Variance
Let \(a,b\) be constants and \(X,Y\) random variables.
- Linear function:
Let \(Y=aX+b\) then \[Var(Y)=Var(aX + b) = a^2Var(X)\] - Sum of independent random variable:
If \(X\) and \(Y\) are independent, \(Var(X+Y) = Var(X)+Var(Y)\).
Moments
For random variable \(X\) and positive integer \(k\), \(E(X^k)\) is called the \(k\)-th moment of \(X\).
Moments provide additional information about the shape of a distribution.
- The first moment about zero: \(E[X]\)
- The second moment about zero: \(E[X^2]\)
- The second moment about the mean is the variance.
Higher moments describe: - Skewness (asymmetry) - Kurtosis (tailedness)
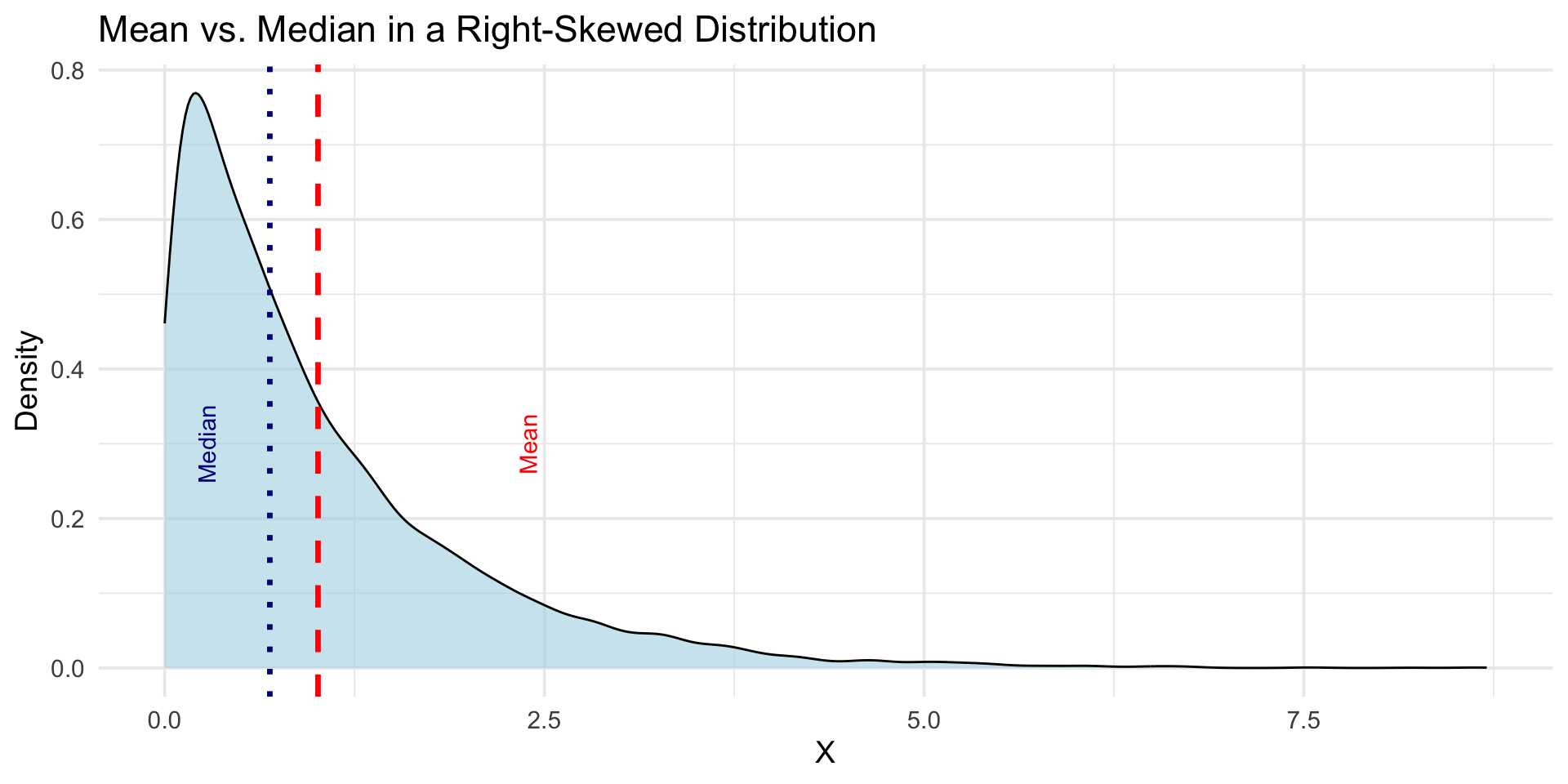
The Mean and the Median
- The mean minimizes squared deviations:
\[E[(X - a)^2]\] is minimized when \(a = E[X].\) - The median minimizes absolute deviations:
\[E[|X - a|]\] is minimized when \(a\) is the median.
For those interested, proof available on SDG pp244-245
The Mean and the Median
Covariance and Correlation
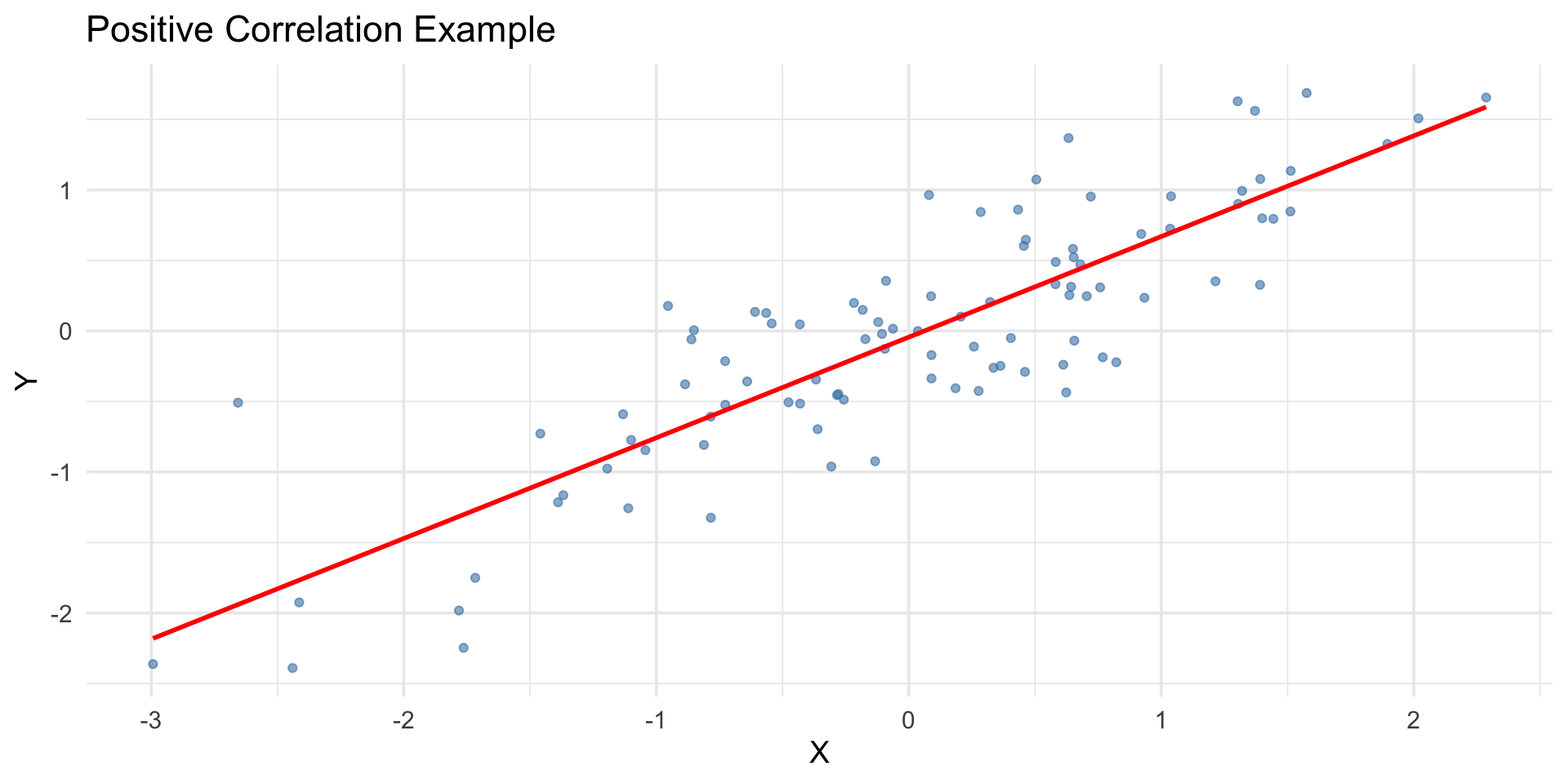
Covariance measures joint variability between two variables: \[Cov(X,Y) = E[(X - E[X])(Y - E[Y])]=E[XY]-E[X]E[Y].\]
Correlation standardizes covariance: \[\rho_{XY} = \frac{Cov(X,Y)}{\sigma_X \sigma_Y}.\]
Property of Covariance and Correlation
Let \(a,b\) be constants and \(X,Y\) random variables.
- Independence:
If \(X\) and \(Y\) are independent, \(Cov(X,Y) = \rho(X,Y)=0\). - Linear function:
Let \(Y=aX+b\) where \(a\neq 0\) then \[\rho(X,Y)=\begin{cases}1 &\text{ if }a>0,\\-1 &\text{ if }a<0.\end{cases}\] - Sum of two random variable:
\(Var(X+Y) = Var(X)+Var(Y)+Cov(X,Y)\).
Visual Example
Conditional Expectation
Conditional expectation is the expected value of \(Y\) given information about \(X\).
\[E[Y|X=x] = \sum_y y \, p_{Y|X}(y|x) \quad \text{or} \quad \int y f_{Y|X}(y|x) dy.\]
It represents the best predictor of \(Y\) given \(X\).
In other words, predictor \(d(X)=E[Y|X]\) minimize the mean squared error (MSE) or \(E[(Y-d(X))^2]\).
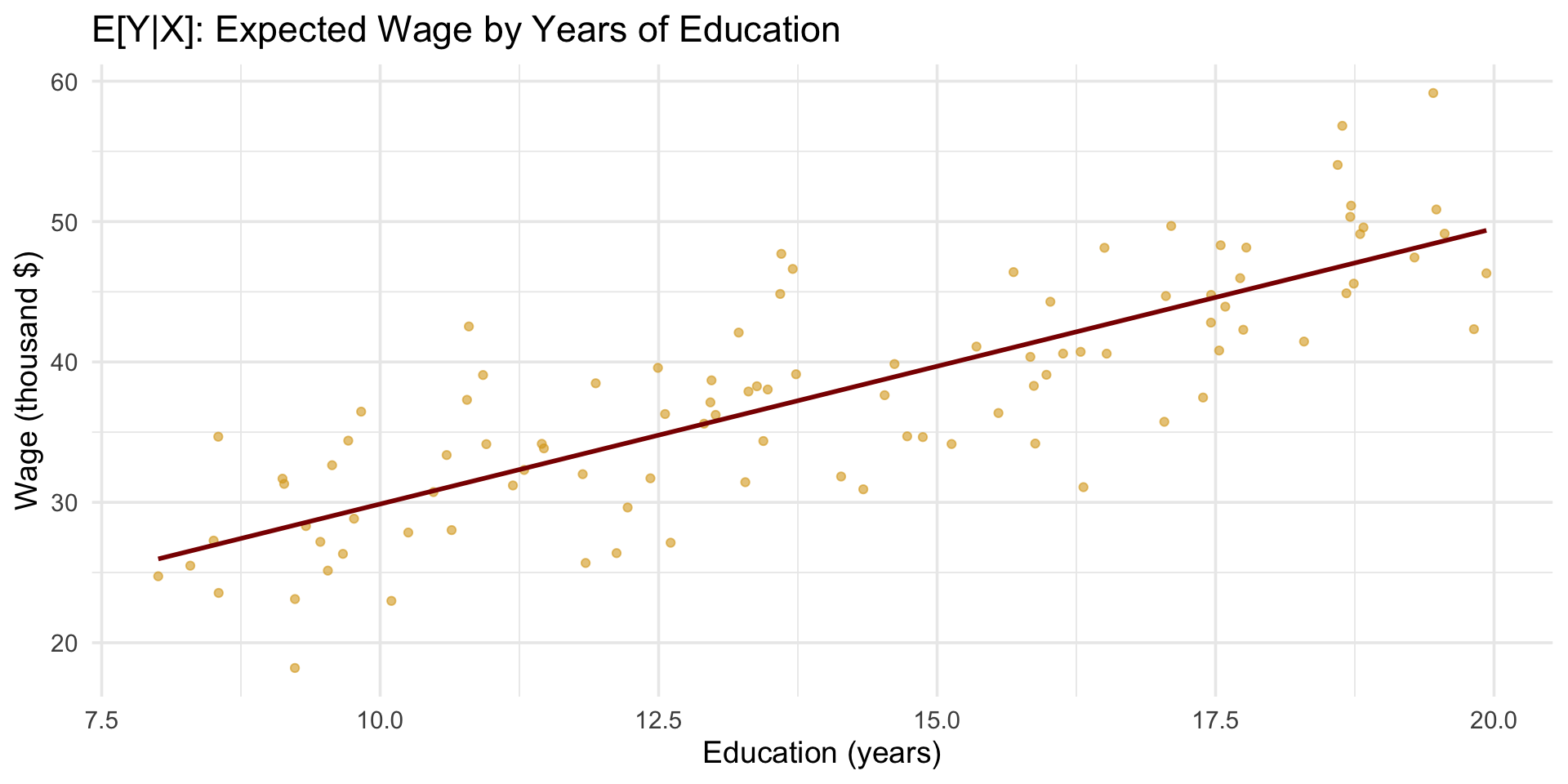
Example: Wage and Education
Let \(Y\) be wage and \(X\) be years of education.
- \(E[Y|X=x]\) gives the expected wage for a person with \(x\) years of education.
- The conditional expectation curve \(E[Y|X]\) is the regression function.
Wrap-Up
| Concept | Definition | Interpretation |
|---|---|---|
| \(E[X]\) | Mean | Long-run average |
| \(Var(X)\) | Variance | Spread around mean |
| \(Cov(X,Y)\) | Covariance | Joint variability |
| \(\rho_{XY}\) | Correlation | Strength of linear relationship |
| \(E[Y|X]\) | Conditional expectation | Best prediction of \(Y\) given \(X\) |
Summary
- Expectation summarizes the “center” of a distribution.
- Variance, covariance, and correlation describe variability and relationships.
- Mean and median differ in skewed data.
- Conditional expectation forms the foundation of regression analysis.
Next lecture: Exam II Review
Fill out this form please

