Model of Continuous Random Variables

Week 8

Maghfira Ramadhani

Oct 08, 2025

Plan

In today’s class we will learn commonly used models for continuous random variables:

  1. Normal random variables
  2. Log-normal random variables
  3. Chi-square random variables
  4. Exponential random variables

Textbook Reference: JA 11; SDG 5.6, 8.2

Continuous random variables

  • Discrete r.v.: take on countable set of values (0,1,2,…).
  • Continuous r.v.: can take on any value in an interval.
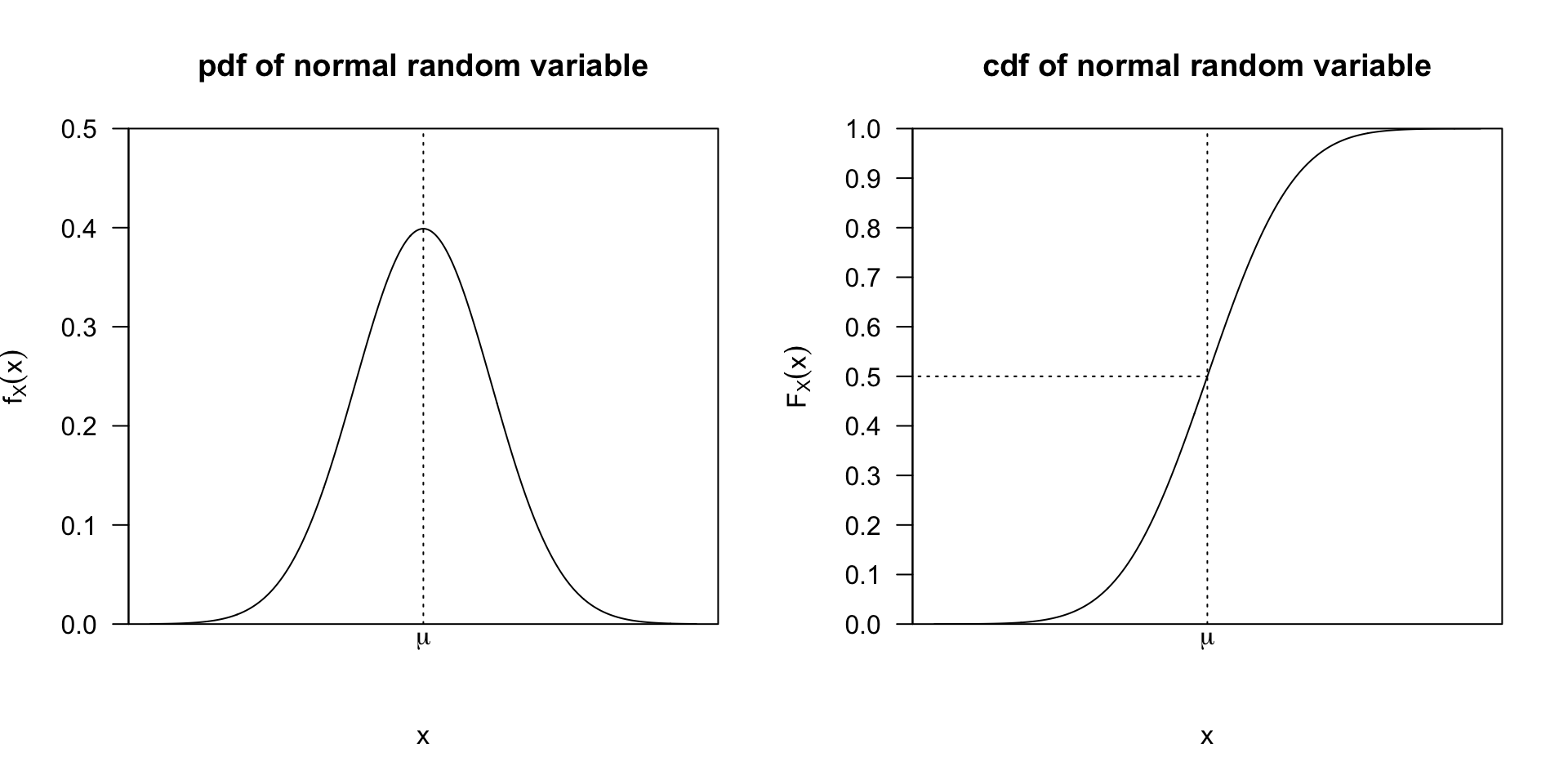
  • Described by a probability density function (pdf) \(f(x)\) such that:

\[ P(a \leq X \leq b) = \int_a^b f(x) dx \]

  • \(f(x)\ge 0\) for all \(x\), and \(\int_{-\infty}^{\infty} f(x) dx = 1\).

Normal random variables

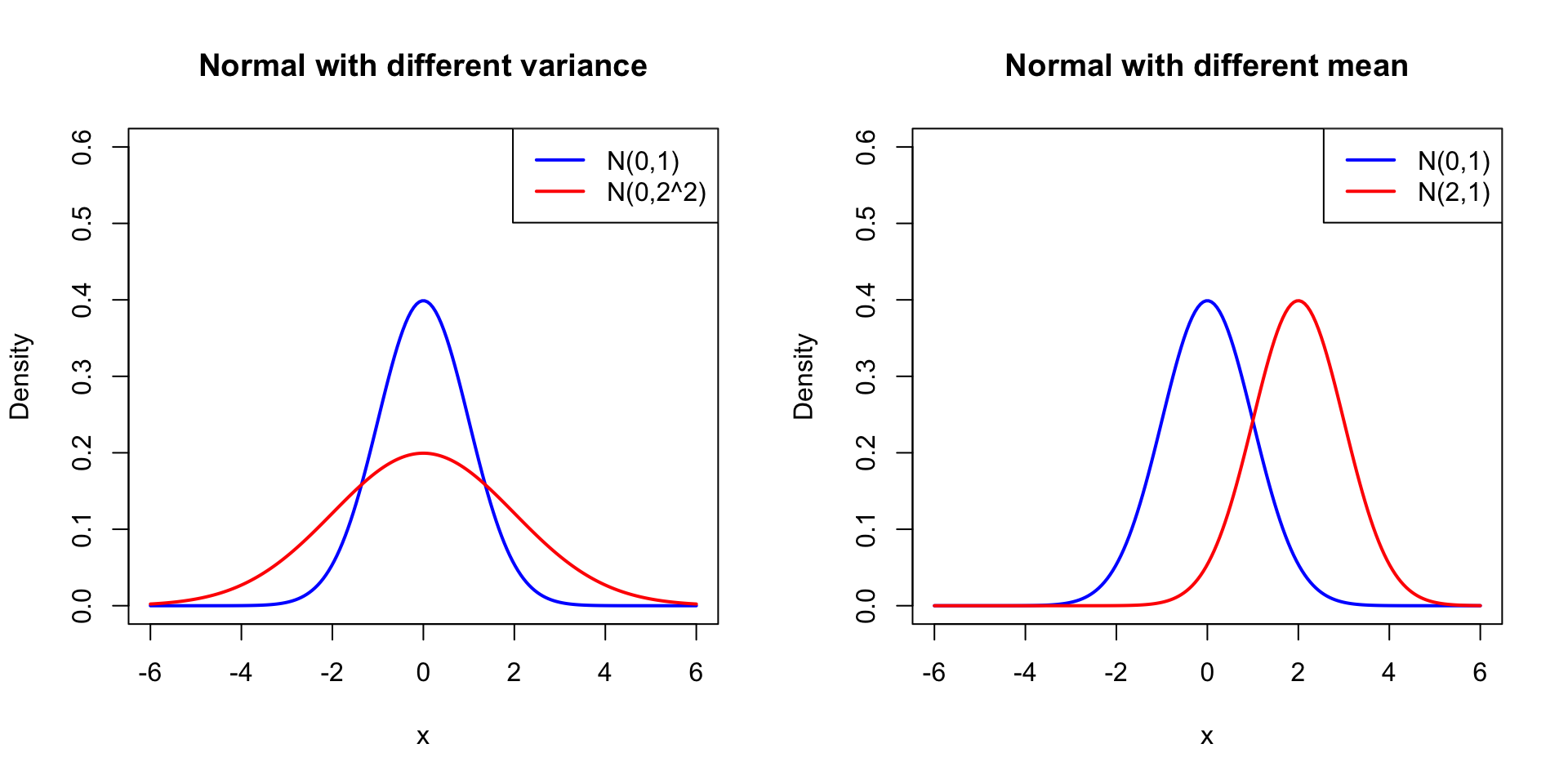
A random variable \(X\) has a normal distribution with mean \(\mu\) and variance \(\sigma^2\), written \(X\sim N(\mu,\sigma^2)\), if its pdf is

\[ f_X(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right). \]

  • Symmetric around \(\mu\), and has a bell-shaped curve.
  • Parameters: mean (\(\mu\)) and variance (\(\sigma^2\)).
  • Functions in R:
pnorm(x,mu,sd) # P(X <= x)
qnorm(p,mu,sd) # quantile at probability p
dnorm(x,mu,sd) # density at x
rnorm(n,mu,sd) # random draws

Normal random variables

Normal random variables

Normal random variables

Standard normal

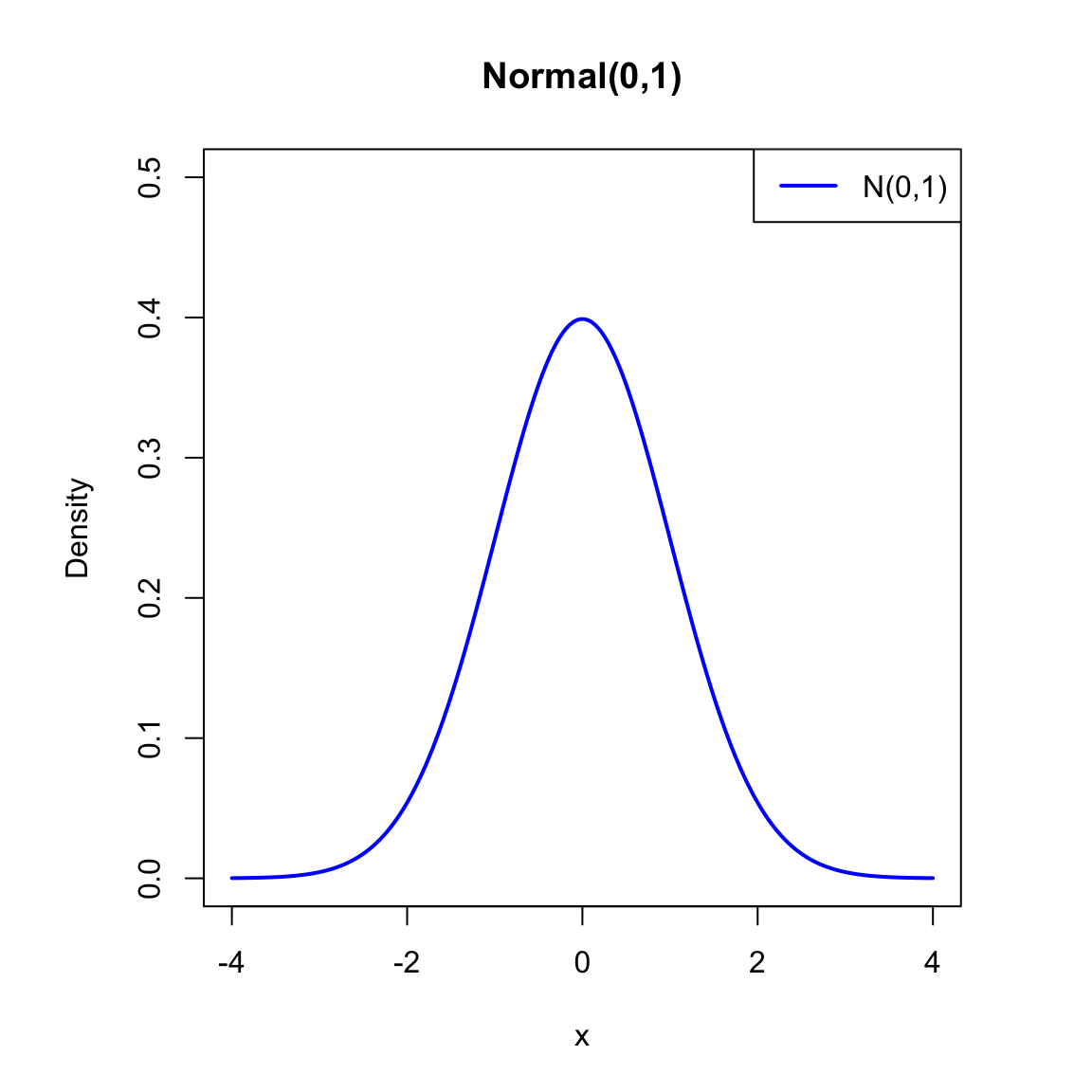
  • If \(X\sim N(\mu,\sigma^2)\), then \(Z=\frac{X-\mu}{\sigma}\sim N(0,1)\).
  • A standard normal pdf denoted \(\phi(z)\) and cdf denoted \(\Phi(z)\)
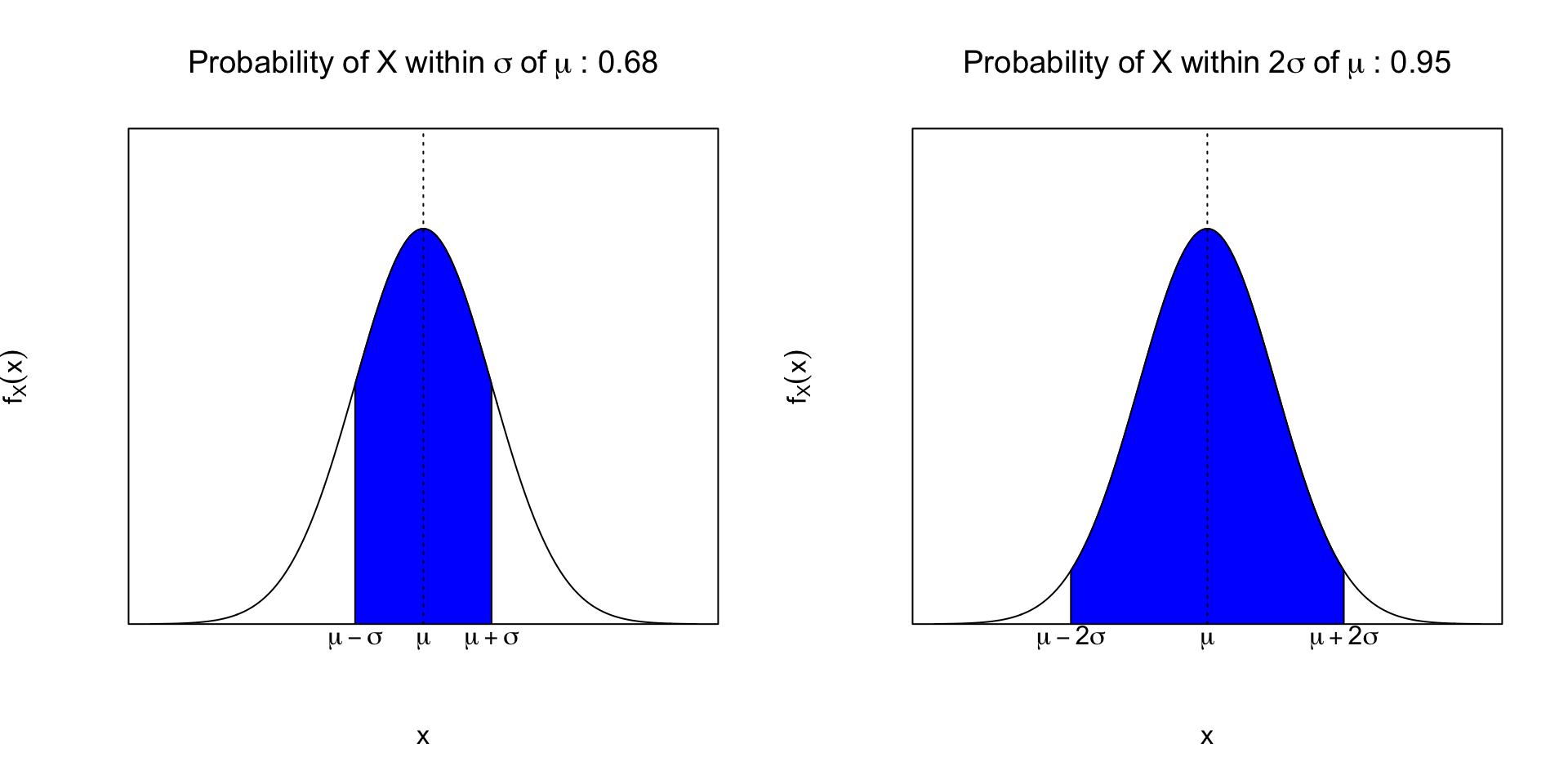
  • Typically used in probability tables/software. \[P(-1.96\leq Z\leq 1.96)\approx 0.95\] \[P(-1.645\leq Z\leq 1.645)\approx 0.90\]
  • Functions in R:
pnorm(z)     # P(Z <= z)
qnorm(p)     # quantile at probability p
dnorm(z)     # density at z
rnorm(n,mu,sd) # random draws

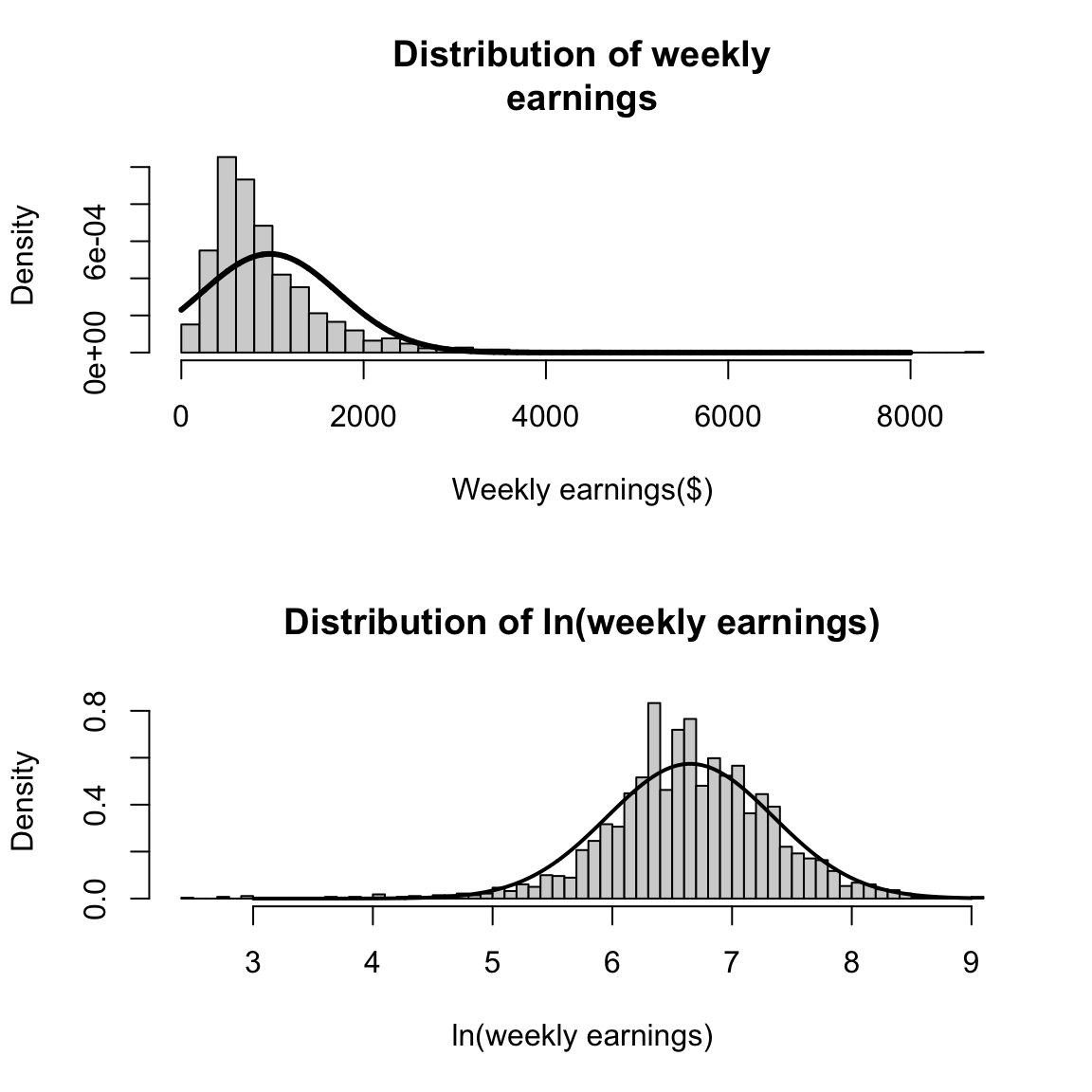
Log-normal random variables

  • If \(\ln X\sim N(\mu,\sigma^2)\),

    then \(X\) is log-normal.

  • \(X\) only takes positive values.

  • Skewed right, long tail.

  • Useful in economics for modeling income, wealth, firm size

  • Functions in R:

plnorm(x,lnmu,lnsd) # P(X <= x)
qlnorm(p,lnmu,lnsd) # quantile at probability p
dlnorm(x,lnmu,lnsd) # density at x
rlnorm(n,lnmu,lnsd) # random draws

Chi-square

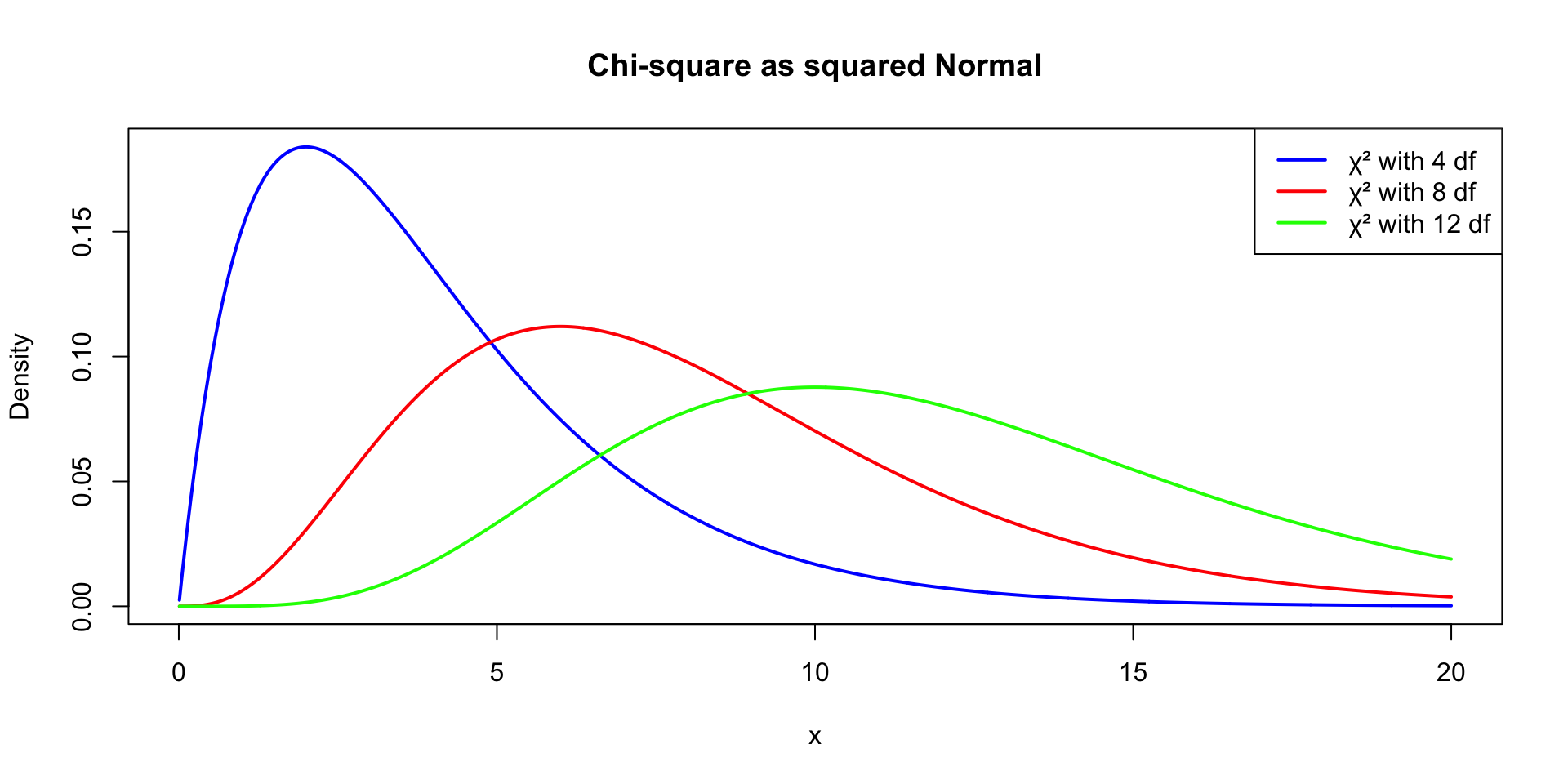
  • If \(Z \sim N(0,1)\), then \(Z^2 \sim \chi^2_1\).
  • More generally, if \(Z_1, Z_2, \ldots, Z_k \sim\) i.i.d. \(N(0,1)\), then

\[ X = Z_1^2 + Z_2^2 + \cdots + Z_k^2 \sim \chi^2_k \]

  • Key relationship: The chi-square distribution is built from the normal.
  • Parameter \(k\) = degrees of freedom.
  • Mean = \(k\), variance = \(2k\).
  • Used in testing (goodness-of-fit, variance tests).
  • Function in R: pchisq(x,df), qchisq(p,df), dchisq(x,df), rchisq(n,df).

Chi-square

Exponential random variables

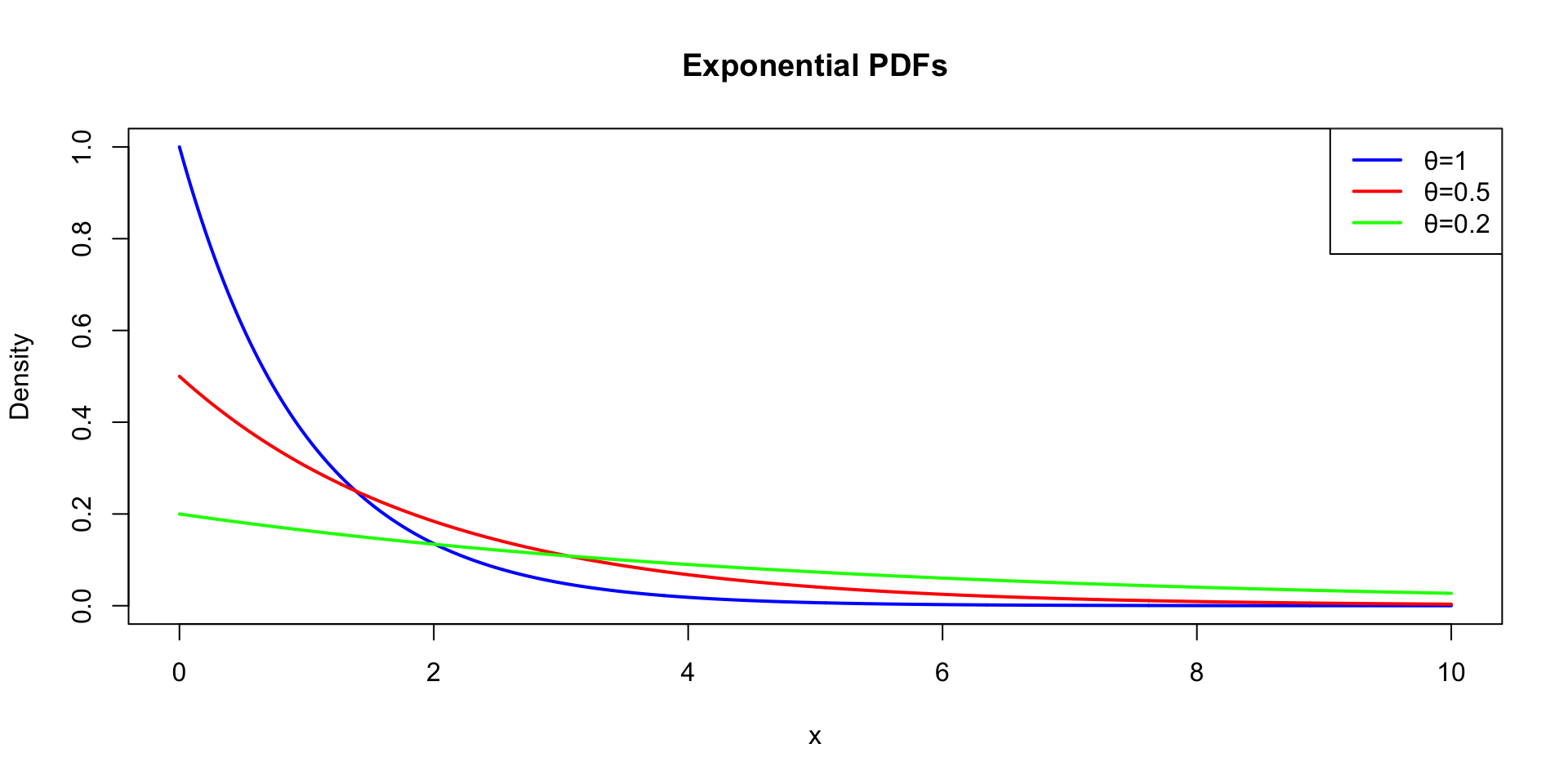
A random variable \(X\) is Exponential (\(\theta\)) if:

\[ f_X(x|\theta) = \theta e^{-\theta x},\quad x\ge 0 \]

  • Mean = \(1/\theta\), variance = \(1/\theta^2\), CDF: \(F_X(x)=1-e^{-\theta x}.\)
  • Applications:
    • Duration of unemployment spells
    • Time until a trade is executed
    • Machine lifetimes
  • Function in R: pexp(x,rate), qexp(p,df), dexp(x,df), rexp(n,df).

Exponential random variables

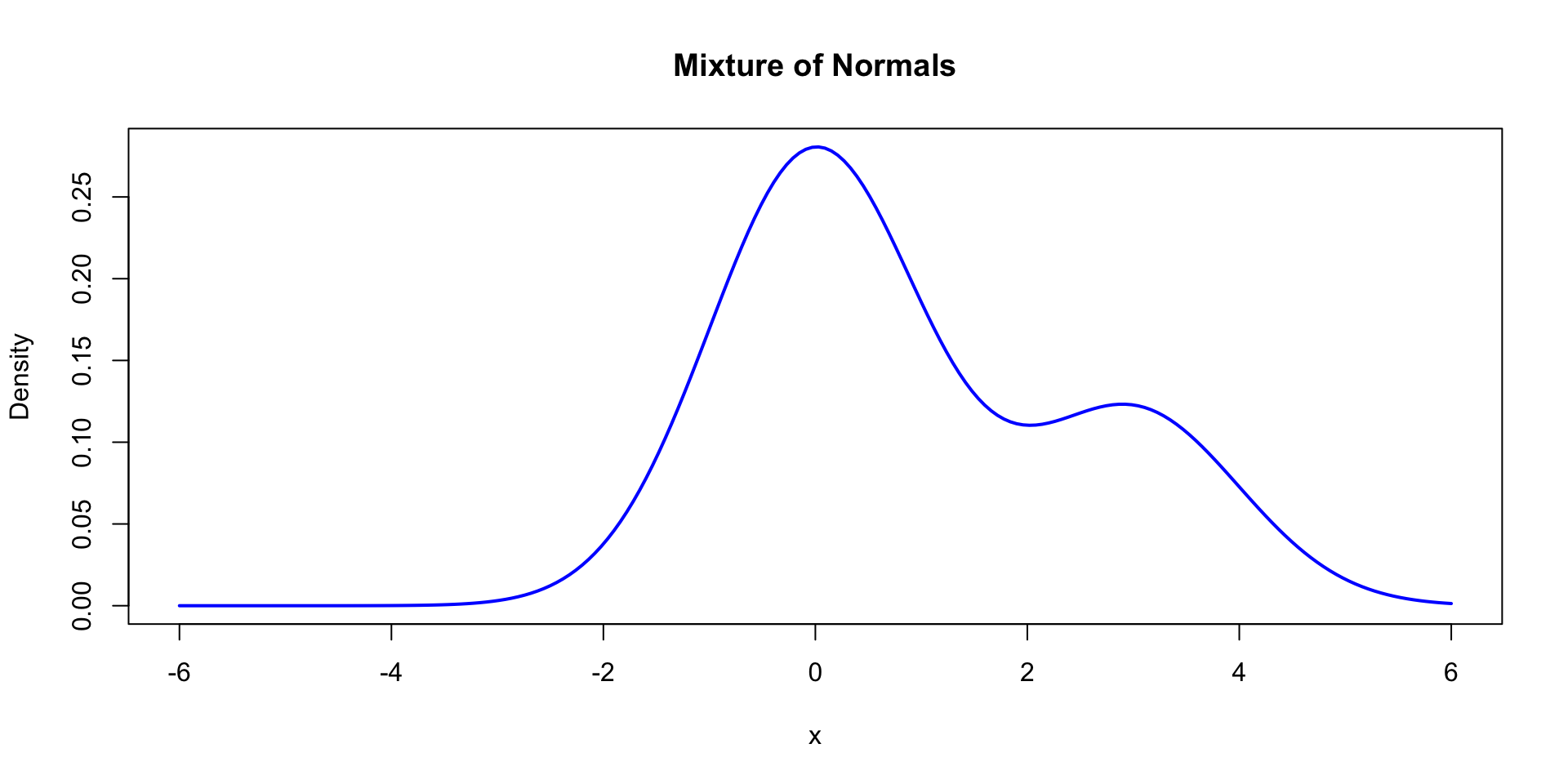
Mixtures of normals

  • Some data look “normal-like” but with multiple peaks.
  • A mixture of normals is a weighted average of normal distributions.

Economic example: distribution of daily sales may differ between weekdays and weekends.

Summary

We learned continuous random variable models:

  • Normal: symmetric, bell-shaped, most common.
  • Lognormal: positive, skewed, used for income/wealth.
  • Chi-square: sums of squared normals, variance testing.
  • Exponential: time durations, memoryless.
  • Mixtures: flexible for multimodal data.

End of Lecture