Lab 5: Simple Linear Regression

Week 14

Maghfira Ramadhani

Nov 17, 2025

Plan

In this lab we will practice:

  1. Visualizing linear relationships
  2. Estimating and interpreting simple linear regression models
  3. Computing slope and intercept manually and using R
  4. Evaluating model fit (R²) and residuals
  5. Reflecting on prediction vs. causality

Textbook Reference: JA Chapter 17

Warm-up & Review

Think about:

- What does the slope represent in a regression line?
- Does correlation imply causation?
- Why do we square residuals in OLS?

Exercise 1: Visualizing a Linear Relationship

Simulated data

set.seed(123)
n <- 100
x <- runif(n, 0, 10)
y <- 5 + 2*x + rnorm(n, 0, 2)
simdata <- tibble(x, y)

Exercise 1: Visualizing a Linear Relationship

ggplot(simdata, aes(x=x, y=y)) +
  geom_point(color="grey40") +
  labs(title="Simulated Data: Y = 5 + 2X + ε",
       x="X", y="Y")

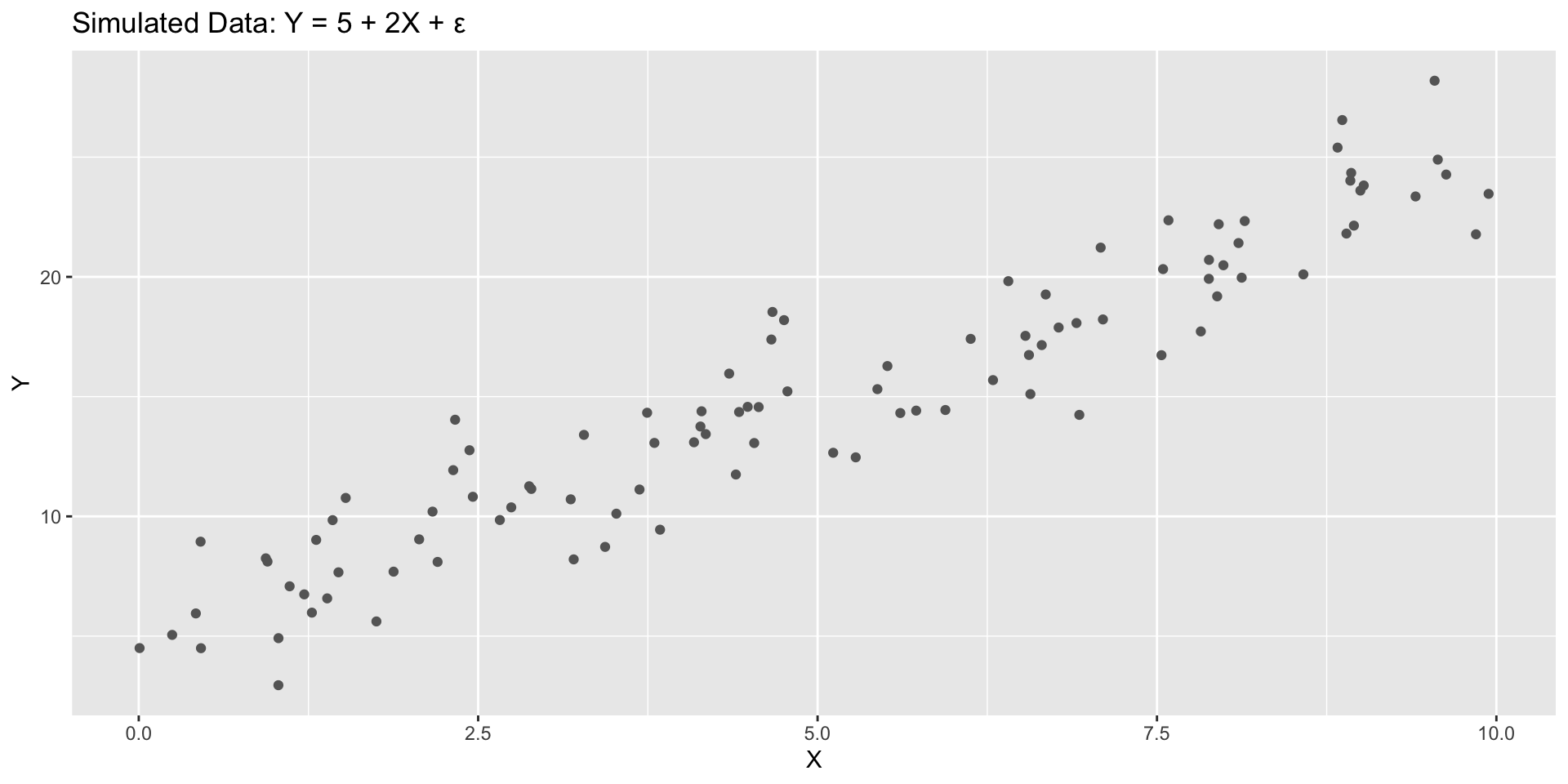
Task 1

Caution

  1. What sign do you expect for the correlation between x and y?
  2. Add a fitted line using geom_smooth(method="lm") and confirm visually.

Exercise 2: Manual OLS Estimation

Compute slope and intercept manually using formulas:

\[ \hat{\beta} = \frac{\sum_i (x_i - \bar{x})(y_i - \bar{y})}{\sum_i (x_i - \bar{x})^2}, \qquad \hat{\alpha} = \bar{y} - \hat{\beta}\bar{x}. \]

beta_hat <- cov(simdata$x, simdata$y) / var(simdata$x)
alpha_hat <- mean(simdata$y) - beta_hat * mean(simdata$x)
c(alpha_hat, beta_hat)
[1] 4.982080 1.982034

Exercise 2: Manual OLS Estimation

Compare with R’s built-in estimator:

model_sim <- lm(y ~ x, data = simdata)
summary(model_sim)

Call:
lm(formula = y ~ x, data = simdata)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.4759 -1.2265 -0.0395  1.1927  4.4345 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  4.98208    0.39211   12.71   <2e-16 ***
x            1.98203    0.06836   28.99   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.939 on 98 degrees of freedom
Multiple R-squared:  0.8956,    Adjusted R-squared:  0.8945 
F-statistic: 840.6 on 1 and 98 DF,  p-value: < 2.2e-16

Task 2

  • Interpret the slope: what does a one-unit increase in \(X\) imply for \(Y\)?
  • How close are your manual and R estimates? Why are they identical (up to rounding)?

Exercise 3: Regression with CPS Data

Question: How does education relate to weekly earnings?

data(cps)
model_cps <- lm(earnwk ~ educ, data = cps)
summary(model_cps)

Call:
lm(formula = earnwk ~ educ, data = cps)

Residuals:
    Min      1Q  Median      3Q     Max 
-1272.1  -417.3  -157.4   229.1  7282.6 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -330.753     72.713  -4.549 5.63e-06 ***
educ         101.550      5.575  18.217  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 709.8 on 2807 degrees of freedom
  (1204 observations deleted due to missingness)
Multiple R-squared:  0.1057,    Adjusted R-squared:  0.1054 
F-statistic: 331.9 on 1 and 2807 DF,  p-value: < 2.2e-16

Task 3

  1. Interpret the slope: how much does weekly earnings increase per year of education?
  2. Is the intercept meaningful here?
  3. Report \(R^2\) and explain what it measures.

Exercise 4: Visualizing the Fit

ggplot(cps, aes(x=educ, y=earnwk)) +
  geom_point(color="grey70") +
  geom_smooth(method="lm", se=FALSE, color="blue") +
  labs(title="Earnings vs Education",
       subtitle="OLS regression line",
       x="Years of Education", y="Weekly Earnings (USD)")

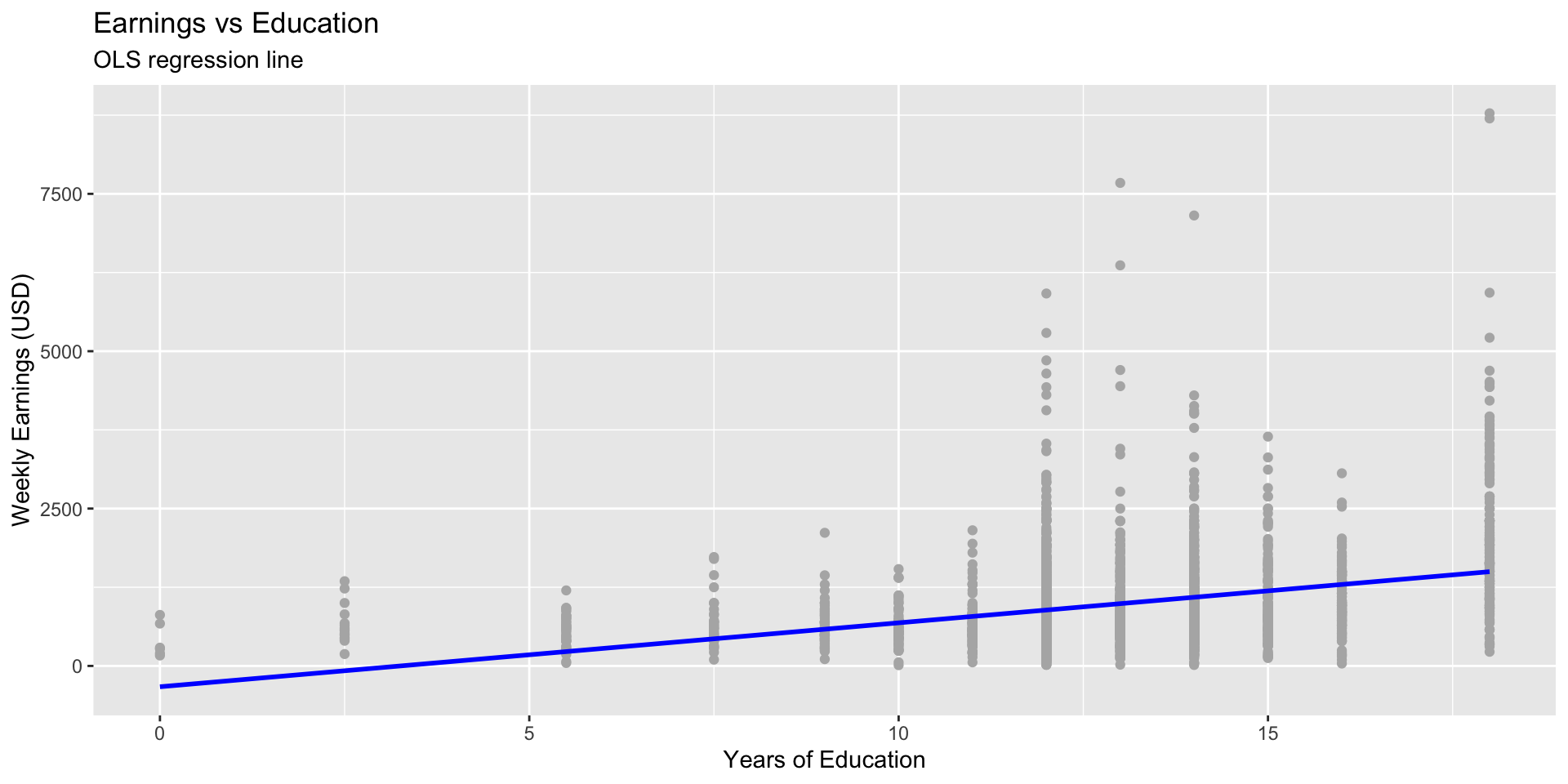
Task 4

  • Add residual lines with geom_segment().
  • Identify one observation with a large positive and one with a large negative residual.
  • What could explain them?

Exercise 5: Prediction and Causality

Use the fitted model to predict average earnings for 12, 14, and 16 years of education.

predict(model_cps, newdata = data.frame(educ = c(12, 14, 16)))
        1         2         3 
 887.8488 1090.9491 1294.0494

Task 5

  • What happens to predicted earnings when education increases by 2 years?
  • Can we interpret this as a causal effect of education on income? Why or why not?
  • What omitted factors might bias the estimate?

Challenge Problem

Simulate a new dataset where \(Y = 5 + 2X + U\) but \(U\) is correlated with \(X\) (e.g., U <- 0.5*X + rnorm(n)).

Estimate the regression again and compare the slope.

Question: Does the estimated slope still recover the true value 2? Why not?

Exit Question

Under what condition can we interpret the slope \(\hat{\beta}\) as a causal effect?

Submission

Submit the rendered PDF or HTML report on Canvas as a group.
Be sure to include your plots, coefficient outputs, and short written interpretations.